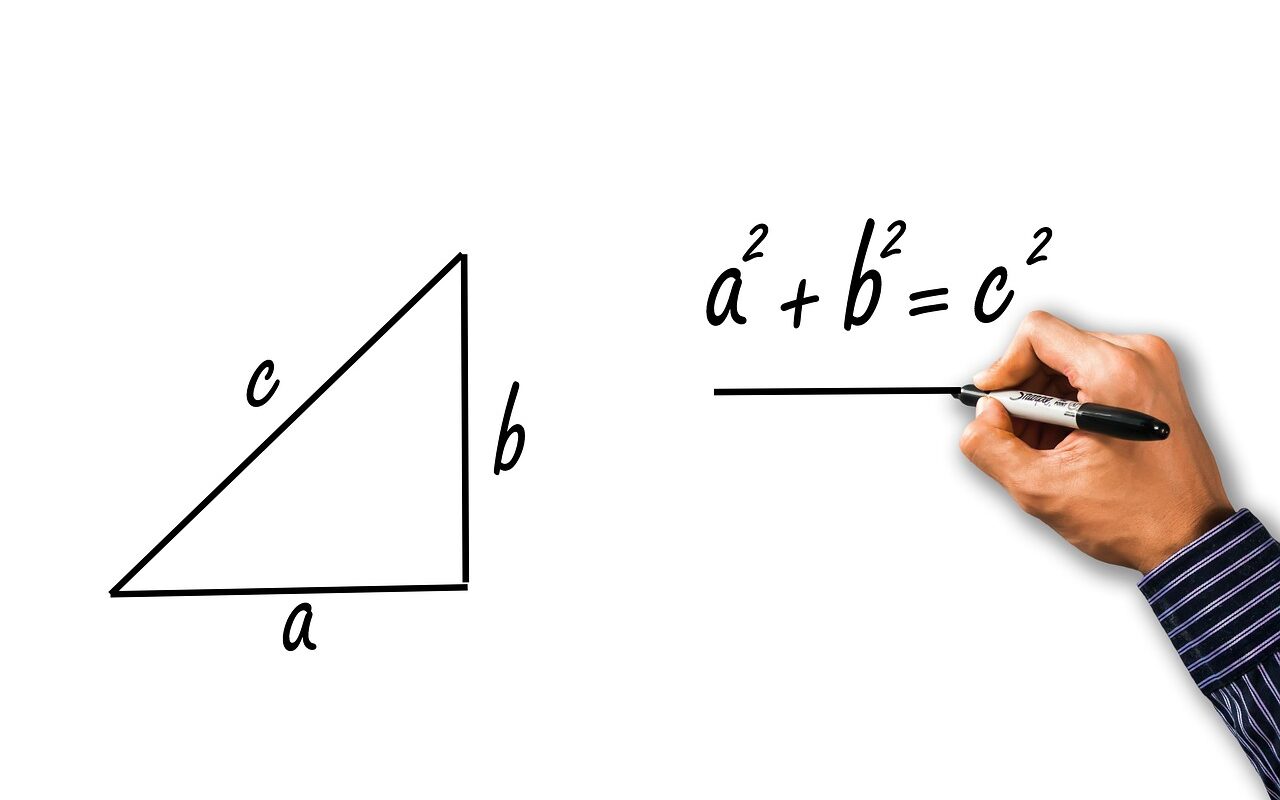Nauka wzorów matematycznych może wydawać Ci się łatwa. Tak jest w rzeczywistości, ale często popełniasz w nauce jeden ważny błąd. Łatwo można się go oduczyć. Zapraszam do wpisu, w którym pokazuję jak uczyć się wzorów matematycznych.
Mam nadzieję, że pamiętasz o karcie wzorów maturalnych, którą możesz wykorzystać na maturze z matematyki. Jeśli jeszcze o niej nie słyszałaś, to zajrzyj tutaj. Sprawne posługiwanie się kartą wzorów oraz samymi wzorami jest bardzo ważne dla dobrego wyniku na egzaminie. Błędy w nauce wzorów mogą w konsekwencji doprowadzić do niezdania matury. Za przykład weźmiemy sobie twierdzenie Pitagorasa, czyli popularny wzór:

Podstawowy błąd w nauce wzorów
Standardowo nauka wzorów matematycznych u każdego przebiega podobnie. Na lekcji poznajesz, skąd się dany wzór wziął (czasem ta część jest pomijana, jeśli jest to zbyt skomplikowane lub nauczyciela goni czas), następnie od szczegółów przechodzisz do samego wzoru, który na samym końcu procesu nauki, starasz się po prostu zapamiętać. Wracając do naszego przykładu z twierdzeniem Pitagorasa, będzie to wyglądało następująco. Nauczyciel zademonstruje Ci poniższy rysunek, a Ty z tego będziesz starała się zapamiętać jedno zdanie. Słynne na całym świecie: „a do kwadratu dodać be kwadratu równa się ce do kwadratu„.

Jeśli właśnie tak uczysz się wzorów matematycznych, to popełniasz standardowy błąd, który może mieć w późniejszych latach poważniejsze konsekwencje. Co zostaje Ci w głowie z takiej definicji? Że masz jakieś a, masz jakieś b i z tego otrzymujesz jakieś c. Z pozoru wszystko wydaje się dość proste, ale… co się stanie, jeśli w zadaniu nie będziesz miała liter a, b lub c? Co zrobisz, gdy litery a, b i c będą na innych miejscach niż w wykutym przykładzie?
Jak uczyć się wzorów matematycznych?
Nie martw się! Alternatywą do standardowej nauki wzorów matematycznych nie jest wcale znajomość każdego zagadnienia od początku aż po stworzenie definicji. Byłoby to wskazane, ale na poziomie podstawowym nie jest wcale konieczne. Ucz się samego wzoru (tak, jak robiłaś to do tej pory), ale rozszerz naukę o to, by wiedzieć, czym jest każda z liter użytych we wzorze. Musisz wiedzieć, że a i b to są przyprostokątne, a c jest przeciwprostokątną. Dzięki temu będziesz umiała przełożyć ten prosty wzór na pełniejszą definicję: „jedna z przyprostokątnych podniesiona do kwadratu dodać druga z przyprostokątnych podniesiona do kwadratu równa się przeciwprostokątna podniesiona do kwadratu”. Na pierwszy rzut oka wygląda może to groźnie i mało zrozumiale, ale to jest właśnie ten krótki wzór rozszerzony o znajomość tego, czym są poszczególne jego składniki (litery).
Dzięki temu zamiana a z c, wprowadzenie np. d i e, nie przeszkodzi Ci w poprawnym zastosowaniu wzoru, bo będziesz wiedziała, czym są jego poszczególne składniki. Ucząc się jedynie krótkiego wzoru, bez zrozumienia tego, co dokładnie tworzy jego treść, zastawiasz na siebie pułapkę. Oczywiście wzór Pitagorasa to tylko przykład. Możemy podać następne: wzór na pole trójkąta to a razy h przez 2, ale warto wiedzieć, że a to podstawa, a h to wysokość padającą na tę (a) podstawę. Zwracam uwagę, że sama wiedza, że h to wysokość to za mało. Musisz wiedzieć, że to wysokość, która pada na naszą podstawę a. Sinus kąta alfa, to a przez c, ale musisz wiedzieć, że a to przyprostokątna naprzeciwko kąta alfa, a c to przeciwprostokątna.
Mam nadzieję, że już teraz rozumiesz to, co chcę Ci przekazać. Oprócz znajomości samego wzoru (lub umiejętności jego znalezienia w karcie wzorów maturalnych) musisz także wiedzieć, czym są poszczególne niewiadome/litery/składniki. Dopiero wtedy możesz mówić, że nauczyłaś się wzorów matematycznych.
Co dalej?
Jeśli masz jakieś pytania, to pisz śmiało w komentarzu pod wpisem lub na Facebooku. Polecam także subskrybować mój kanał na YouTube, bo już od przyszłego tygodnia zaczną się tam pojawiać pierwsze materiały, które mogą Ci pomóc w przygotowaniu do poprawy matury z matematyki. Jeśli maturę z matematyki zdajesz dopiero w przyszłym roku (lub później), to także polecam obserwować. Razem damy radę!